How to make Mathematics much easier

Use What You Know to Find What You Don’t

What’s 9 × 6? You might know the answer straight away — 54. But how did you get there? Maybe you just remembered it. Or maybe you used a trick without even realising.

Let’s say you don’t know your 9 or 6 times tables. No problem. You probably know your 10s. And 9 is just one less than 10. So you could do 10 × 6 = 60. Then subtract one group of 6. That’s 60 – 6 = 54.

It’s the same with adding. What’s 28 + 89? That’s a bit clunky. But you can make the numbers friendlier. Add 1 to 89 to get 90. Then take 1 from 28 to get 27. Now do 90 + 27. Much easier — that’s 117.

You could also do it the other way: add 11 to 89 to get 100, take 11 from 28 to get 17. Add those: 100 + 17 = 117. Either way, you break a hard problem into simpler steps.

Maths Is About Making Connections

Good maths isn’t about remembering a hundred different facts. It’s about spotting relationships between numbers and being able to use this knowledge. If you can use what you already understand, you can find out what you don’t yet understand. This learning strategy is called constructivism and is explained in Teaching Student-Centered Mathematics by Van de Walle and co thusly:

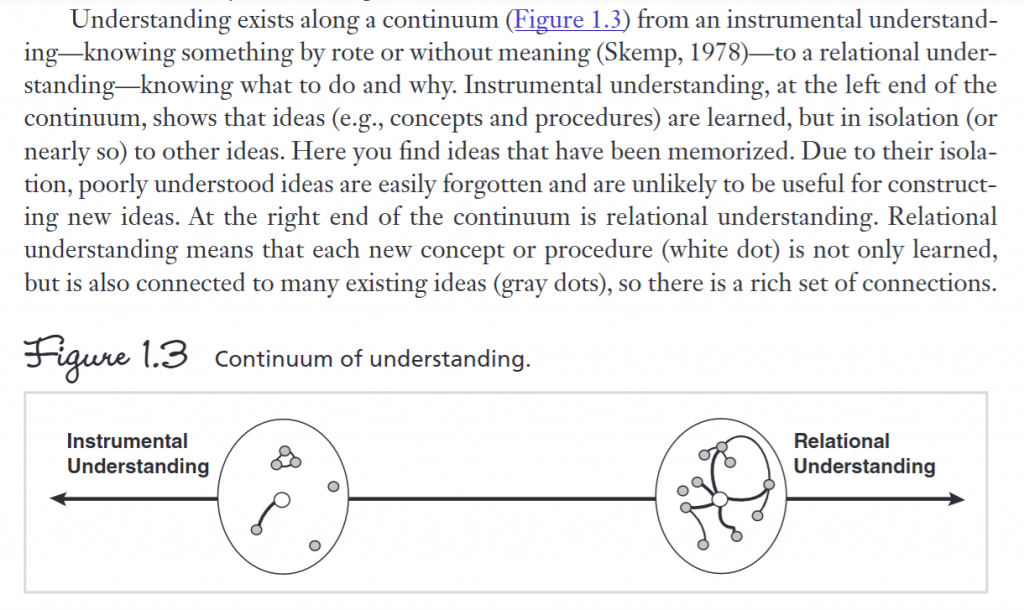
Counting Is Harder Than You Think

Going back to our arithmetic problems, one thing I’ve realised that counting is actually very hard. In the context of an arithmetic problem, relying only on counting will make things much slower and harder for learners.

Let’s go back to 9 + 8. To find the sum, you could count up – 10, 11, 12… all the way up to 17. That’s a lot of steps. Very early learners will of course begin with this strategy because it’s the most obvious. But it’s essential that they move on from this.

One way I did this with my children is by focusing on doubles facts. Once a child is fluent with doubles facts up to 10 (i.e. 1 x 2 is 2, 2 x 2 is 4, etc), they can bring their knowledge to 8 + 9. They know that 8 + 8 makes 16, so the sum of 9 + 8 must be one more because 9 is one more than 8. These strategies are much faster and use far less mental effort than counting.

Help Children Think Flexibly

When dong arithmetic exercises with children, we should encourage them to spot patterns and call on their previous knowledge. We can prompt them with statements and questions like:

• What number is 9 close to?
• Can you get to an easier number to help?
• Can you break the number into smaller chunks?
• What would happen if you changed it slightly?

Gradually, children will start to build their flexibility with numbers. They’ll learn that there are many different strategies they can use to work through a problem. They’ll become much more engaged in the process of searching for ways through mathematical exercises. And this can only be good news for them as they develop into confident, independent mathematical thinkers.

Try it at home and watch your child rise, just like Imhotep!