The Equal sign as “The Answer Comes Next”
Ask most children and adults what the equal sign means and you’ll likely hear, “That’s where the answer goes.” But studies show that seeing the equal sign as a prompt to write an answer has a serious impact on children’s mathematical understanding, especially when it comes to algebra and reasoning.
Researchers tell us that children often struggle with mathematical sentences that don’t follow the familiar “a + b = c” format. For example, many children cannot solve or make sense of a sentence like 8 + 4 = __ + 5, because it doesn’t match the pattern they’ve been trained to expect. This isn’t because the maths is too hard — it’s because their understanding of the equal sign is limited.
Two Views of the Equal Sign
In a key study, researchers found two dominant interpretations among pupils:
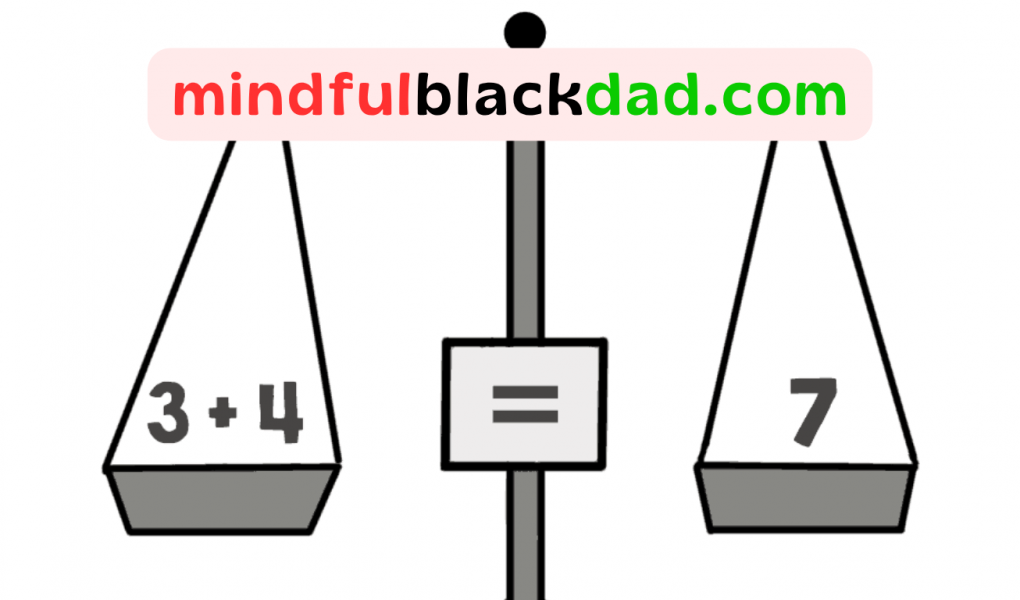
- Operational Understanding: The equal sign means “do the operation and write the answer.”
- Relational Understanding: The equal sign shows that the two sides are of equal value — a balance.
By Year 6, most children still held an operational view. And even by Year 8, nearly half were still stuck in it. The consequences are clear. When children only think operationally, they’re less likely to succeed in algebra, struggle with more complex equations, and fail to grasp the deeper structure of mathematics.
Why It Matters
A relational understanding of the equal sign is crucial for algebra and all higher-level mathematical thinking. In algebra students need to manipulate both sides of an equation — not just “do” one side and write an answer. Equations in science work the same way. Whether it’s F = ma or E = mc², these are relationships, not instructions.
Children who see the equal sign as a relationship see maths as about thinking and comparing, not just chasing answers.
Textbooks reinforce wrong view of Equal Sign
Most textbooks and worksheets reinforce the operational view by presenting only problems like 6 + 2 = __. Very few include equations like __ = 6 + 2 or 4 + 3 = 2 + __, which require relational thinking. Pupils also learn to read from left to right and are rarely asked to look at an equation as a whole.
Yet when given concrete objects even young children show they do understand the concept of equality. The issue lies not with the child, but with how we teach the symbol.
It comes as no surprise to learn that in China, children are taught the relational understanding of the equal sign. This is one of the key factors behind their generally impressive mathematical performance.
What We Can Do
- Use Concrete Models: Great for physically representing balanced equations
- Use Varied Formats: Introduce equations like 5 = 2 + 3 and 6 + 1 = 4 + 3 from early on
- Talk in Terms of Balance: Shift the language from “What’s the answer?” to “What would make both sides equal?”
Maths Is About Reasoning, Not Just Answers
Mathematics isn’t a race to find the final number. It’s a way of thinking about relationships, structure, and patterns.
Let’s stop treating “=” as just a stepping stone to an answer. And let’s start treating it as the foundation of deep mathematical thinking.
